[ Spreadsheets @ https://drive.google.com/open?id=0B1iBvkbdWzq0RUtNcGsyanFBVjg ]
I was getting very confused by the apparently weird behavior of the BLE discovery mechanism. There are three basic parameters that govern how much power gets used, and how how long, on average, it takes for one peer to discover another. Explanations on the web are confusing, and always seem to omit some vital piece of information. I got so confused, that I decided to make a simulator to try and figure it out. It’s subtle.
Here is a chart showing the advertising cycle. Milliseconds are on the x-axis. In this example the radio is advertising 5% of the time. Each 3-transmission operation takes less than 1ms. The chart title starts with 4 numbers in parentheses. These represent, in order, the scan window, the scan interval, the advertising period, and the advertising interval. More about scanning in a moment.
So I can begin to compare different strategies I have defined a measurement I call a “power unit”. It assumes that transmitting and receiving are equally expensive (which is approximately true).
 |
| Advertising for 1ms every ~20ms |
Notice that the advertising events are not quite evenly distributed. If two peers transmit at exactly the same time, their packets will “collide” and receivers will get corrupted data. So advertising packets are transmitted at an interval that includes a random delay (in the range 0-10ms), so if multiple advertisers start advertising at the same moment, they will eventually drift out of synch. with each other. Advertising packets are short, and are transmitted on three different frequencies.
The radio does scan and advertise at the same time. If it did it would just hear it’s own transmissions anyway. When simultaneously scanning, and advertising, I discovered that scanning events take precedence, and the relatively shorter advertising events are rescheduled for a random time after the scanning operation completes. So activity looks like this:
 |
| Scanning for 12ms every 36ms, and advertising for 1ms every ~20ms |
Notice there is a big gap between the first two advertising events. This happened because the second advertising event was scheduled for 46ms which fell inside the second scan event, so it was delayed by a fixed+random amount. The rescheduled advertising event then landed at 74ms, which was inside the 3rd scan event, and so it was delayed for a second time, finally appearing at 99ms.
Now it’s quite possible for an advertising event to continue being blocked over many scanning events. Here is a pathological case where the advertiser is blocked for about 300ms.
 |
| Scanning and advertising at the same specified interval |
Under some circumstance this could go on for even longer, and the advertiser would never be discovered!
It turns out that this is solved by only only allowing a maximum of ten advertising packets to be blocked before the scanner is told to miss a turn. I was unable to provoke this behavior so I wonder how often it really occurs.
Discovery
So the big question, of course, is how do these parameters impact the time it takes to discover a peer device, and thus in turn, what the impact on the power budget is.
Here are two peers who are both advertising and scanning on the “pathological” schedule.
 |
| Max latency 357ms, and 129 power-units |
The advertisements that are “discovered” are tagged with a ‘*’ on the top axis.
What this illustrates is the time it takes for a scanner to hear the peer’s advertisement. I call this the latency. The average latency can be quite small, but what matters from a “reliability” standpoint is the maximum latency. This determines how long a peer had to both advertise and scan to be heard. I should stress that is not a theoretical result (my math isn’t good enough). It is a result gained by simulating the system for many cycles.
Let’s go with my assumption that transmitting and receiving cost about the same amount of power per unit of time. In the first two-peer example the radio is on for 36% of a possible maximum 212ms. I’ll call that a maximum of 212*0.36 = 77 units of power to guarantee discovery.
What if we advertised more often?
 |
| Colliding packets are marked with ‘X’ |
In the latest example, another snag crops up. Packets are being transmitted so often that they start to collide. But in spite of this the maximum latency drops and the power required goes down dramatically to 32 because the latency is much lower.
As a reality check would advertising 8x less frequently use less power because there are fewer transmissions, or more power because the latency goes up.
 |
| Less, or more power if we advertise less often? |
Advertising is fast (1ms), but now there are fewer chances for the scanner to hear the advertisement, so the maximum latency goes up dramatically to 260 ms. and it costs 90 units.
So how about scanning more often to make it more likely that the scanner hears the advertiser?
Now the advertiser finds it hard to sneak an advertisement into the scanning schedule. So few advertising packets make it out, and the latency goes through the roof.
So where is the sweet spot?, where both latency and power is low. Here it says,
“For non-connectable beacons, the (advertising) interval cannot be smaller than 100 ms. For connectable beacons, it cannot be smaller than 20 ms.”
Our beacons will be connectable, so let’s start with 20ms.
Lengthening the advertisement interval to required minimum of 20ms
So this is certainly not better, and may be worse. So obviously I have to crank down the amount of time spent scanning. But where is the sweet spot?
Repeating the simulation while holding the scan interval constant at 60ms, varying the Scan Window, and running over long sample periods I ended up with the following graph. It has a very obvious, and mysterious sweet-spot at 32ms. I’m not feeling very confident about this plot.
 |
| An obvious scan-window sweet spot at 32ms |
Even more advertisements
To get a fix in 3D it is neccessary to range with four other units. So there are five peers in play in this example. I have kept the scanning and advertising parameters the same, but simply increased the number of peers.
A few packets collide now, which pushes up the max latency, and power quite a bit. It’s important to remember that this example is somewhat bogus because in this case we don’t actually consider which peer discovers the advertiser. In practice, of course, an advertiser will want to get discovered by each peer in turn, and then range them to get a fix. Anyway, in spite of their being 5 peers now, the maximum latency is 129ms, but the radios are only on for 58% of the time so the cost is 75 units.
Directed discovery
So let’s return to the simple 2-peer example, with our evolved parameters.
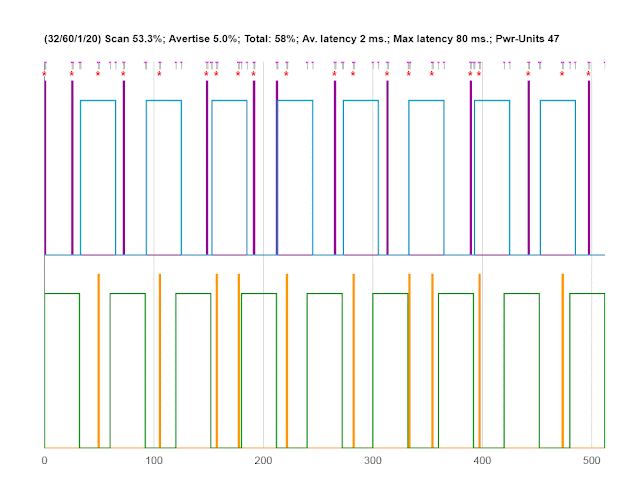 |
| Both peers are advertising, and discovering each other
Notice that both peers are advertising, and discovering each other.
Now let’s assume that the top peer in the diagram is interested in discovering the bottom peer, but not vice-versa. I call that “Directed scanning” or “Dir-Scan” in the diagram title. Another way of putting this is that the bottom-peer wants to be discovered by the top peer. Notice that the ‘*’ markers are only above the upper-peer’s scans. The difference in the statistics is down to insufficient sampling.
Now let’s bump the number of peers up to 5 again, keeping the same parameters, and having each peer scan for any other peer, and see what it looks like.
Now let’s repeat this in Dir-Scan mode. In this case each peer is only interested in advertisments from the peer below – except for the bottom peer which tracks the top peer.
The maximum latency, and Power have gone up a lot. We would expect the average latency to go up by about a factor of 2. Because a scanner will hear the desired advertiser within one cycle, 25% of the time; within 2-cycles 25% of the time… and within 4 cycles the rest of the time. So on average it will take (1+2+3+4)/4 cycles = 2.5 times longer. Our experimental data produces 5? Maybe insufficient samples, or is my thinking faulty? The maximum latency goes up by 60%, and the power by a similar amount.
In fact it isn’t this bad because on the first scan any peer is acceptable. On the second scan 3 of the 4 are acceptable, then 2/4, then 1/4. So the max latency on the first will be 189ms, and the last max latency will be 297ms, A wet finger estimate says 1.2 seconds worst case, and best case around 50-60ms.
Repeating the Dir-Scan simulation while holding the scan interval constant at 60ms, varying the Scan Window and running over long sample periods I ended up with the following graph.
Maybe it would be a bit smoother if I calculated over a greater number of samples? Anyway, minimum energy seems to be somewhere around 27ms.
The pattern looks like this.
Unfortunately
The parameters that seem to work out well above, are not acceptable to the BLE API. Why this is makes no sense, but suggests my simulator is broken in some fundamental way!
Here are parameters that are acceptable, and work.
Notice that the scan parameters are now 4ms every 80ms. The extra line in the title will make more sense when I demonstrate the latest upgrade. Notice too, that there are a quite a lot of collisions when the simulation runs for a while. That statistic is a bit misleading because it measures the total number of collisions seen by all the peers. Obviously each peer only sees a collision in which it is involved, so in this case the total % should be divided by 2.
I wanted to know how long it would take for one peer to discover all of the other peers. The simulator ignores repeated discoveries until all of the peers have been discovered. In the above example the statistics on the second line of the title are for discovering all of the other peers, where n=1, so it is the same as the simple discovery.
For 3 peers the collision count is about the same. Each peer will on average see half that, but there is a remote chance that all three peers will collide of course.
So as we might expect, the time to discover any other peer goes down, because there are twice as many possibilities. We might expect the time to discover both peers would be twice as long, but it’s ought to be a little less than that because initially we don’t care which peer we hear from first.
Here is an example with 3,4 and 5 peers.
With 4 peers the time to find any other peer goes down again, and the time to find all of the others goes up. The collision rate is about the same.
With 5 peers the worst-case time to discover them all gets up above 11 seconds. The % of collisions is slightly higher as we might expect. Reductio ad absurdum says that if there are an infinite number of transmitters, then no peer will ever get a word in.
|



















